압축의 종류
희소 배열 (Sparse Array) 압축
예를 들어, char mName [128] 같은 배열인 경우 이름을 128바이트 꽉꽉 채워서 사용하는 경우는
굉장히 드물것이다. 따라서 이처럼 내용을 다 채우지 못하는 컨테이너 같은 것들이 쉽게 건질 수
있는 최적화 대상이므로 압축할 필요가 있다.
여기서 mName과 같이 널 종료 문자열인 경우에는 std::strlen() 함수를 써서 그 길이만큼만
Write 하면 수신 측에서 길이만큼 컨테이너를 확장해서 사용할 수 있다.
void Write(OutputMemoryStream& inStream)const
{
uint8_t nameLength = static_cast<uint8_t>(strlen(mName));
inStream.Write(nameLength);
inStream.Write(mName, nameLength);
}길이를 먼저 알려주는 이유는 수신자가 스트림에서 얼마나 데이터를 읽어야 하는지 알려주려는 의도이다.
캐시 적중률 관점에서 최적화를 위해 객체의 이름을 std::string 같은 것으로 표현하는 게 훨씬 효율적이다.
그러면 128바이트 공간을 차지해야 할 때보다 캐시 메모리의 적은 분량만 차지하면 되므로 캐시 적중률이
높아질 것이다.
캐시 적중률(Cache Rate)란?
캐시 메모리가 있는 컴퓨터 시스템은 CPU가 메모리에 접근하기 전에 캐시 메모리에서 원하는 데이터의 존재 여부를 확인한다. 이때 필요한 데이터가 있는 경우를 적중(HIT), 없는 경우를 실패(miss)라고 한다.
적중률 = (캐시 메모리 적중 횟수) / (전체 메모리 참조 횟수)이다.
보통 CPU는 데이터를 가져오기 위해 캐시 메모리 > 메모리 > 보조 기억장치 순으로 접근한다.
- 캐시 적중일 때 : 캐시 메모리의 데이터를 CPU 레지스터에 복사한다.
- 캐시 실패/ 메모리 적중일 때 : 메모리의 데이터를 캐시 데이터에 복사하고, 캐시 메모리에 복제된 내용을 CPU 레지스터에 복제한다.
- 캐시, 메모리 실패일 때 : 보조 기억장치에서 필요한 데이터를 메모리에 복사한다. 메모리에 복사된 내용을 캐시 메모리에 복제하고 캐시 메모리에 복제된 내용을 CPU 레지스터에 복사한다.
위의 char [128] -> string의 변환은 128 바이트에서 일부 공간만 실제 데이터가 담겨 있는 것에 반해서
실제 데이터가 담긴 길이만큼만을 사용하기 때문에 적중률이 높아지는 것이다.
엔트로피 인코딩
엔트로피 인코딩이란, 데이터 압축에 있어 출현하는 데이터의 예측 가능성 정도가 얼마나 높고 낮은 가에 따라 압축률이 달라진다는 이론이다. 효율적인 인코딩을 위해서 특정 값이 다른 값보다 빈번하게 등장하는 멤버 변수를 직렬화 하는 것에 사용된다. 예를 들어서, 게임 내 캐릭터가 대부분 땅에 붙어 있어서 Y축 이동이 거의 일어나지 않는 경우이다.
void Write(const Vector3& inVector)
{
Write(inVector.mX);
Write(inVector.mY);
Write(inVector.mZ);
}
void WritePos(const Vector3& inVector)
{
Write(inVector.mX);
Write(inVector.mZ);
if (inVector.mY == 0)
Wrtie(true);
else
{
Write(false);
Write(inVector.mY);
}
}원래 대로라면 총 48비트를 전송해야 하지만
밑의 함수로 고쳐 쓴 경우, 대부분은 1비트 만을 전송하게 될 것이다.
물론 최악의 경우에는 33비트(32 +1)를 전송할 수도 있다. 하지만 게임 내 통계 추적을 통해서
플레이어가 대부분 바닥에 있었다면 압도적인 수치로 비트 수가 압축될 수 있다.
예를 들어서 플레이 타임의 90%가 바닥에 붙어 있는 경우
P(바닥) X Bits(바닥) + P(공중) X Bits(공중) = 0.9 x 1 + 0.1 x 33 = 4.2
Y 값을 직렬화 하는데 필요한 기대 비트 수가 32비트에서 4.2로 줄어들었다!
물론 이런 식으로 값에 따라 처리를 하는 코드를 늘여놓다 보면 굉장히 더러운 코드가 될 것이다.
이를 해결하기 위해서 '간이 허프만 코딩'을 구현하는 것이 보편적이다.
허프만 코딩이란?
허프만 코딩이란, 문자의 빈도 또는 확률 정보를 이용해 통계적 압축을 하는 방법이다.
예를 들어서 문자열 'AAABBCD'에 대해서 살펴보자면
A가 3번
B가 2번
C, D가 1번씩 출현한다.
빈도수가 높은 부호에는 짧은 코드를 대응시키고
빈도수가 낮은 부호에는 긴 코드를 대응시키며 필요한 공간을 최소화시킨다.
여기서는 A에 짧은 코드를 대응시키고 C, D에 긴 코드를 대응시킨다.
등장하는 문자는 'A, B, C, D'로 3bit 코드로 모든 문자를 대응시킬 수 있다.
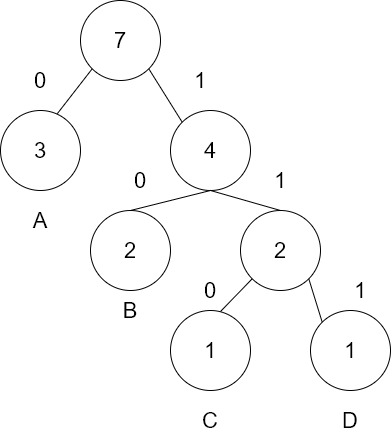
원 안에 들어있는 숫자는 문자열에서 나타난 문자의 횟수이고, 원 밑의 숫자들은 부호화하기 위한 비트 값이다.
빈번하게 나온 순서대로 가까운 위치에 배치된다. 이를 테이블 형식으로 만들어 보자.
| 문자 | 코드 |
| A | 0 |
| B | 10 |
| C | 100 |
| D | 101 |
위의 내용에서, 많은 경우를 처리하고 싶을 땐 기댓값에 대한 조회 테이블을 두고, 여러 개의 비트를 묶어
이 비트열이 뜻하는 숫자를 위와 같이 테이블에 대한 인덱스로 기록하는 식으로 간이 허프만 코딩을 구현
하면 될 것이다.
고정소수점
흔히 쓰이는 유용한 방법으로, 보내려는 수치의 가능 범위 및 요구 정밀도를 파악한 다음 고정소수점 형식으로
변환하면 비트 수를 최소화하여 보낼 수 있다.
예를 들어서, 월드의 좌표가 4000 x 4000 단위 정도이며, 월드 중심이 좌표계의 원점 즉 (0,0,0)에 있다는 걸
알아냈다. 이를 해석하면 X 및 Z 축의 최솟값은 -2000이고, 최댓값은 2000이라는 뜻이다.
게임 플레이 테스트를 해 본 결과 좌표 이동은 0.1 단위 정도의 정밀 도면 충분하다는 것을 알아냈다.
이러한 조건들이 파악됐다면 다음과 같은 공식으로 X, Z 축에 가능한 값의 최대 개수를 산할 수 있다.
(최댓값 - 최솟값) / 정밀도 + 1 = (2000 -(-2000))/0.1 +1 = 40001
log2(40001) = 15.3 이므로, X와 Z에 각각 16비트만 있으면 직렬 화할 수 있다.
고정 소수점에 대한 표현 방식은 위의 내용을 벗어나므로, 여기를 클릭해서 내용을 숙지하기 바란다.
기하 압축
어떤 변수에 허용되는 값의 범위에 제약이 있다면, 더 적은 양의 비트로 그 정보를 표현할 수 있다!
여러 가지 기하 자료형이 이에 해당된다. 예를 들어 사원수가 이에 해당된다.
사원수란?
사원수는 네 개의 부동소수점 숫자로 구성된 자료형으로, 삼차원 공간에서 회전을 나타낼 때 유용하다.
압축의 관점에서 중요한 것은 사원수로 회전을 표현할 때 정규화한다는 것으로 즉, 각 성분이
-1~1 값이고 또한 각 성분을 제곱하여 모두 더한 값이 1이라는 것이다.
사원수를 직렬 화할 때는 네 성분 중 셋만 처리하고, 넷째 성분은 1비트로 부호만 표시하면 된다.
직렬화를 풀어 읽어 들일 때는 세 성분 값을 읽어 들여 제곱해 더한 다음, 더한 값을 1에서 빼면
넷째 성분을 살려낼 수 있다.
'게임 서버 프로그래밍 > 네트워크 개념정리' 카테고리의 다른 글
| IOCP 공부 노트: (1) _beginthreadex , CreateThread (0) | 2020.07.10 |
|---|---|
| 객체 리플리케이션 (0) | 2020.03.02 |
| 직렬화 (0) | 2020.02.24 |
| NAT과 P2P (0) | 2020.02.19 |
| TCP (Transmission Control Protocol) (0) | 2020.02.19 |